¿Qué es el p-valor?

Este post tiene como finalidad explicar el concepto de p-valor, su definición y para mayor entendimiento usar un ejemplo práctico. Para empezar vamos a definir formalmente el concepto de p-valor.

La definición formal de p-valor es:

p-valor (p-value en inglés) se define como la probabilidad de que un valor estadístico calculado sea posible dada una hipótesis nula cierta. En términos simples, el p-valor ayuda a diferenciar resultados que son producto del azar del muestreo, de resultados que son estadísticamente significativos.

– wikipedia.org

Puede que sea confuso, así que lo explicaremos paso a paso. Para ello necesitamos saber los conceptos de hipótesis nula e hipótesis alternativa.

Para que el método científico funcione es necesario definir una hipótesis de investigación, siendo esta hipótesis contrastada con información recolectada a través de la observación.

En el lenguaje estadístico, las hipótesis pueden ser tanto nula como alternativa; la hipótesis alternativa equivale al complemento de la hipótesis nula. A modo de ejemplo, una hipótesis nula es afirmar que el costo mensual per cápita en transporte en Chile es de 40000 CLP \((= 40000 )\); entonces la hipótesis alternativa es el costo per cápita mensual en transporte en Chile es distinto a 40000 CLP \(( \neq 40000 )\).

Entonces, hasta ahora tenemos una hipótesis que quiero contrastar con lo observado y su estado en la naturaleza (verdadera ó falsa). Cuando queremos contrastar las hipótesis, tenemos los siguientes escenarios.

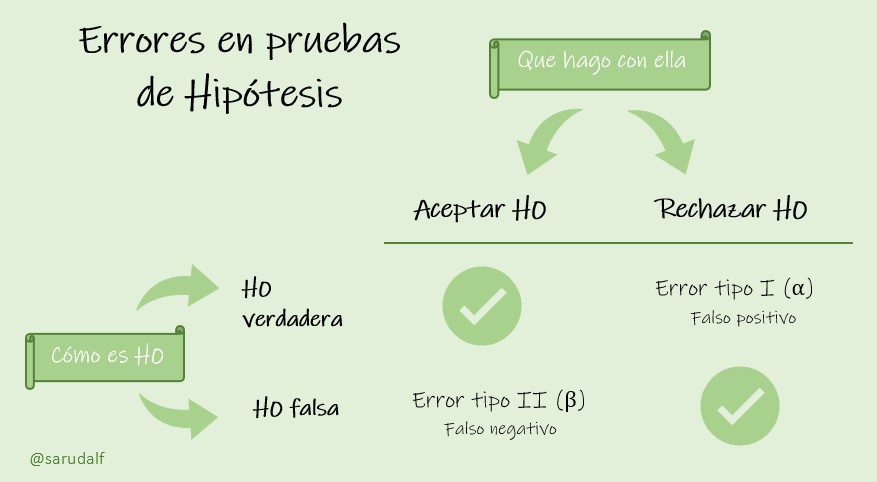
Hay dos casos en los que uno puede errar, estos son llamados error tipo I y II. Estos casos son ejemplificados en la siguiente figura.

Nuestro objetivo es decidir si la hipótesis de investigación es rechazada o aceptada. El p-valor es la probabilidad de cometer error tipo I (Rechazar H0 cuando este es verdadero).

Para realizar el cálculo necesitamos la información recolectada por la observación, y que llamaremos muestra. En los casos más simples de pruebas de hipótesis, se asume que está debe ser iid (independientes e identicamente distribuidas), y para que la muestra sea representativa de la población, esta debe ser aleatoria.

Cada problema de pruebas de hipótesis tiene asociado un estadístico de prueba, y este es calculado usando la información de la muestra y de la hipótesis nula. Por ejemplo, para el caso de una prueba de hipótesis para la media con \(\sigma\) conocido y \(n>30\), tenemos que el estadístico de prueba es el siguiente:

siendo \(\mu\) definida en la hipótesis nula.

En modo abstracto, el p-valor es la probabilidad del estadístico de prueba (Nota: conocer hipótesis unilateral y bilateral).

Siguiendo nuestro ejemplo, asumimos que se seleccionó una muestra de tamaño 30 con un promedio de gasto de 40500 CLP y una desviación estándar poblacional de 1650 CLP, entonces tenemos que el estadístico de prueba es igual a

Al observar la hipótesis alternativa (bilateral), tenemos que calcular la probabilidad en ambas colas, es decir,

Ahora que calculamos el p-valor, ¿como lo interpretamos? ¡la parte más importante de este post!

En cada prueba de hipótesis, tenemos que comparar el p-valor con un nivel de significación (\(\alpha\)), donde la el críterio es el siguiente

Si \(\alpha > \text{p-valor}\), se rechaza H0
Si \(\alpha \leq \text{p-valor}\), se no se rechaza H0

Una deducción del críterio de decisión es el siguiente:

\(\text{p-valor alto}\): los datos son probables con una hipótesis nula verdadera.
\(\text{p-valor bajo}\): los datos son poco probables con una hipótesis nula verdadera.

Concluyendo nuestro ejemplo, tenemos que para un nivel de significación del 5% \((\alpha=0.05)\) se rechaza H0, es decir, hay evidencia en la muestra que el costo per cápita es diferente a 40000; mientras que para un nivel de significación del 10% \((\alpha=0.10)\) no se rechaza la hipótesis nula.

Debes saber que hay muchos test de hipótesis, dónde lo más importante es identificar la hipótesis nula, el estadístico de prueba y la función de distribución de probabilidad del estadístico de prueba bajo H0.